7.3 Problem-Solving
Learning Objectives
By the end of this section, you will be able to:
- Describe problem solving strategies
- Define algorithm and heuristic
- Explain some common roadblocks to effective problem solving
People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.
The study of human and animal problem solving processes has provided much insight toward the understanding of our conscious experience and led to advancements in computer science and artificial intelligence. Essentially much of cognitive science today represents studies of how we consciously and unconsciously make decisions and solve problems. For instance, when encountered with a large amount of information, how do we go about making decisions about the most efficient way of sorting and analyzing all the information in order to find what you are looking for as in visual search paradigms in cognitive psychology. Or in a situation where a piece of machinery is not working properly, how do we go about organizing how to address the issue and understand what the cause of the problem might be. How do we sort the procedures that will be needed and focus attention on what is important in order to solve problems efficiently. Within this section we will discuss some of these issues and examine processes related to human, animal and computer problem solving.
PROBLEM-SOLVING STRATEGIES
When people are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.
Problems themselves can be classified into two different categories known as ill-defined and well-defined problems (Schacter, 2009). Ill-defined problems represent issues that do not have clear goals, solution paths, or expected solutions whereas well-defined problems have specific goals, clearly defined solutions, and clear expected solutions. Problem solving often incorporates pragmatics (logical reasoning) and semantics (interpretation of meanings behind the problem), and also in many cases require abstract thinking and creativity in order to find novel solutions. Within psychology, problem solving refers to a motivational drive for reading a definite “goal” from a present situation or condition that is either not moving toward that goal, is distant from it, or requires more complex logical analysis for finding a missing description of conditions or steps toward that goal. Processes relating to problem solving include problem finding also known as problem analysis, problem shaping where the organization of the problem occurs, generating alternative strategies, implementation of attempted solutions, and verification of the selected solution. Various methods of studying problem solving exist within the field of psychology including introspection, behavior analysis and behaviorism, simulation, computer modeling, and experimentation.
A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them (table below). For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.
| Method | Description | Example |
|---|---|---|
| Trial and error | Continue trying different solutions until problem is solved | Restarting phone, turning off WiFi, turning off bluetooth in order to determine why your phone is malfunctioning |
| Algorithm | Step-by-step problem-solving formula | Instruction manual for installing new software on your computer |
| Heuristic | General problem-solving framework | Working backwards; breaking a task into steps |
Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?
A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):
- When one is faced with too much information
- When the time to make a decision is limited
- When the decision to be made is unimportant
- When there is access to very little information to use in making the decision
- When an appropriate heuristic happens to come to mind in the same moment
Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.
Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.
Further problem solving strategies have been identified (listed below) that incorporate flexible and creative thinking in order to reach solutions efficiently.
Additional Problem Solving Strategies:
- Abstraction – refers to solving the problem within a model of the situation before applying it to reality.
- Analogy – is using a solution that solves a similar problem.
- Brainstorming – refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal solution is reached.
- Divide and conquer – breaking down large complex problems into smaller more manageable problems.
- Hypothesis testing – method used in experimentation where an assumption about what would happen in response to manipulating an independent variable is made, and analysis of the affects of the manipulation are made and compared to the original hypothesis.
- Lateral thinking – approaching problems indirectly and creatively by viewing the problem in a new and unusual light.
- Means-ends analysis – choosing and analyzing an action at a series of smaller steps to move closer to the goal.
- Method of focal objects – putting seemingly non-matching characteristics of different procedures together to make something new that will get you closer to the goal.
- Morphological analysis – analyzing the outputs of and interactions of many pieces that together make up a whole system.
- Proof – trying to prove that a problem cannot be solved. Where the proof fails becomes the starting point or solving the problem.
- Reduction – adapting the problem to be as similar problems where a solution exists.
- Research – using existing knowledge or solutions to similar problems to solve the problem.
- Root cause analysis – trying to identify the cause of the problem.
The strategies listed above outline a short summary of methods we use in working toward solutions and also demonstrate how the mind works when being faced with barriers preventing goals to be reached.
One example of means-end analysis can be found by using the Tower of Hanoi paradigm. This paradigm can be modeled as a word problems as demonstrated by the Missionary-Cannibal Problem:
Missionary-Cannibal Problem
Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.
Hint: At one point in your solution, you will have to send more people back to the original side than you just sent to the destination.
The actual Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape. The objective of the puzzle is to move the entire stack to another rod obeying the following rules:
- 1. Only one disk can be moved at a time.
- 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
- 3. No disc may be placed on top of a smaller disk.
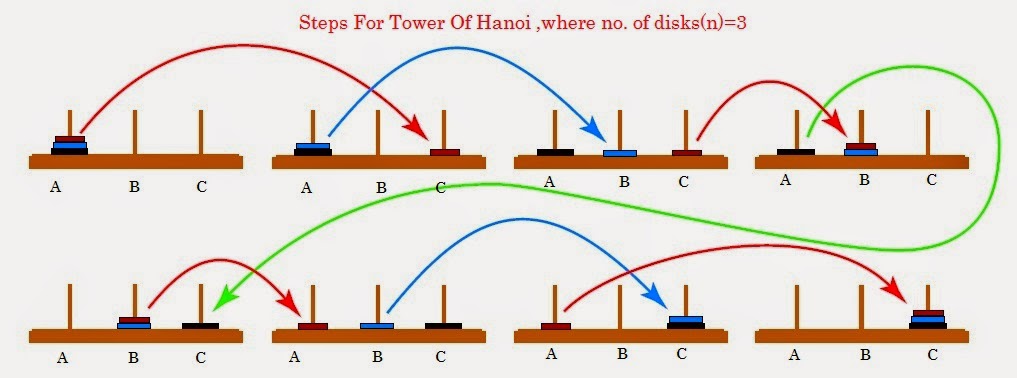
Figure 7.02. Steps for solving the Tower of Hanoi in the minimum number of moves when there are 3 disks.
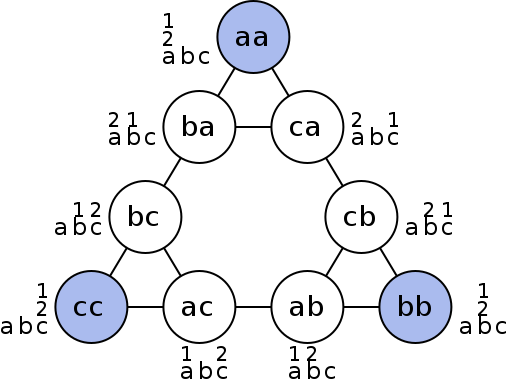
Figure 7.03. Graphical representation of nodes (circles) and moves (lines) of Tower of Hanoi.
The Tower of Hanoi is a frequently used psychological technique to study problem solving and procedure analysis. A variation of the Tower of Hanoi known as the Tower of London has been developed which has been an important tool in the neuropsychological diagnosis of executive function disorders and their treatment.
GESTALT PSYCHOLOGY AND PROBLEM SOLVING
As you may recall from the sensation and perception chapter, Gestalt psychology describes whole patterns, forms and configurations of perception and cognition such as closure, good continuation, and figure-ground. In addition to patterns of perception, Wolfgang Kohler, a German Gestalt psychologist traveled to the Spanish island of Tenerife in order to study animals behavior and problem solving in the anthropoid ape.
As an interesting side note to Kohler’s studies of chimp problem solving, Dr. Ronald Ley, professor of psychology at State University of New York provides evidence in his book A Whisper of Espionage (1990) suggesting that while collecting data for what would later be his book The Mentality of Apes (1925) on Tenerife in the Canary Islands between 1914 and 1920, Kohler was additionally an active spy for the German government alerting Germany to ships that were sailing around the Canary Islands. Ley suggests his investigations in England, Germany and elsewhere in Europe confirm that Kohler had served in the German military by building, maintaining and operating a concealed radio that contributed to Germany’s war effort acting as a strategic outpost in the Canary Islands that could monitor naval military activity approaching the north African coast.
While trapped on the island over the course of World War 1, Kohler applied Gestalt principles to animal perception in order to understand how they solve problems. He recognized that the apes on the islands also perceive relations between stimuli and the environment in Gestalt patterns and understand these patterns as wholes as opposed to pieces that make up a whole. Kohler based his theories of animal intelligence on the ability to understand relations between stimuli, and spent much of his time while trapped on the island investigation what he described as insight, the sudden perception of useful or proper relations. In order to study insight in animals, Kohler would present problems to chimpanzee’s by hanging some banana’s or some kind of food so it was suspended higher than the apes could reach. Within the room, Kohler would arrange a variety of boxes, sticks or other tools the chimpanzees could use by combining in patterns or organizing in a way that would allow them to obtain the food (Kohler & Winter, 1925).
While viewing the chimpanzee’s, Kohler noticed one chimp that was more efficient at solving problems than some of the others. The chimp, named Sultan, was able to use long poles to reach through bars and organize objects in specific patterns to obtain food or other desirables that were originally out of reach. In order to study insight within these chimps, Kohler would remove objects from the room to systematically make the food more difficult to obtain. As the story goes, after removing many of the objects Sultan was used to using to obtain the food, he sat down ad sulked for a while, and then suddenly got up going over to two poles lying on the ground. Without hesitation Sultan put one pole inside the end of the other creating a longer pole that he could use to obtain the food demonstrating an ideal example of what Kohler described as insight. In another situation, Sultan discovered how to stand on a box to reach a banana that was suspended from the rafters illustrating Sultan’s perception of relations and the importance of insight in problem solving.
Grande (another chimp in the group studied by Kohler) builds a three-box structure to reach the bananas, while Sultan watches from the ground. Insight, sometimes referred to as an “Ah-ha” experience, was the term Kohler used for the sudden perception of useful relations among objects during problem solving (Kohler, 1927; Radvansky & Ashcraft, 2013).
Solving Puzzles
Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (see figure) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.
How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)
Here is another popular type of puzzle (figure below) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:
Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.
Take a look at the “Puzzling Scales” logic puzzle below (figure below). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

What steps did you take to solve this puzzle? You can read the solution at the end of this section.
PITFALLS TO PROBLEM SOLVING
Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.
Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.
Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).
In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.
The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.
Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision. Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the table below.
| Bias | Description |
|---|---|
| Anchoring | Tendency to focus on one particular piece of information when making decisions or problem-solving |
| Confirmation | Focuses on information that confirms existing beliefs |
| Hindsight | Belief that the event just experienced was predictable |
| Representative | Unintentional stereotyping of someone or something |
| Availability | Decision is based upon either an available precedent or an example that may be faulty |
Were you able to determine how many marbles are needed to balance the scales in the figure below? You need nine. Were you able to solve the problems in the figures above? Here are the answers.

SUMMARY
Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.
References:
Openstax Psychology text by Kathryn Dumper, William Jenkins, Arlene Lacombe, Marilyn Lovett and Marion Perlmutter licensed under CC BY v4.0. https://openstax.org/details/books/psychology
Exercises
Review Questions:
1. A specific formula for solving a problem is called ________.
a. an algorithm
b. a heuristic
c. a mental set
d. trial and error
2. Solving the Tower of Hanoi problem tends to utilize a ________ strategy of problem solving.
a. divide and conquer
b. means-end analysis
c. analogy
d. experiment
3. A mental shortcut in the form of a general problem-solving framework is called ________.
a. an algorithm
b. a heuristic
c. a mental set
d. trial and error
4. Which type of bias involves becoming fixated on a single trait of a problem?
a. anchoring bias
b. confirmation bias
c. representative bias
d. availability bias
5. Which type of bias involves relying on a false stereotype to make a decision?
a. anchoring bias
b. confirmation bias
c. representative bias
d. availability bias
6. Wolfgang Kohler analyzed behavior of chimpanzees by applying Gestalt principles to describe ________.
a. social adjustment
b. student load payment options
c. emotional learning
d. insight learning
7. ________ is a type of mental set where you cannot perceive an object being used for something other than what it was designed for.
a. functional fixedness
b. confirmation bias
c. working memory
d. insight learning
Critical Thinking Questions:
1. What is functional fixedness and how can overcoming it help you solve problems?
2. How does an algorithm save you time and energy when solving a problem?
Personal Application Question:
1. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?
Glossary:
algorithm
anchoring bias
availability heuristic
confirmation bias
functional fixedness
heuristic
hindsight bias
mental set
problem-solving strategy
representative bias
trial and error
working backwards
Answers to Exercises
Review Questions:
1. A
2. B
3. B
4. A
5. C
6. D
7. A
Critical Thinking Questions:
1. What is functional fixedness and how can overcoming it help you solve problems?
2. How does an algorithm save you time and energy when solving a problem?
Glossary:
algorithm: problem-solving strategy characterized by a specific set of instructions
anchoring bias: faulty heuristic in which you fixate on a single aspect of a problem to find a solution
availability heuristic: faulty heuristic in which you make a decision based on information readily available to you
confirmation bias: faulty heuristic in which you focus on information that confirms your beliefs
functional fixedness: inability to see an object as useful for any other use other than the one for which it was intended
heuristic: mental shortcut that saves time when solving a problem
hindsight bias: belief that the event just experienced was predictable, even though it really wasn’t
mental set: continually using an old solution to a problem without results
problem-solving strategy: method for solving problems
representative bias: faulty heuristic in which you stereotype someone or something without a valid basis for your judgment
trial and error: problem-solving strategy in which multiple solutions are attempted until the correct one is found
working backwards: heuristic in which you begin to solve a problem by focusing on the end result



