Read the scenario below and think about how effective the lesson might have been.

---

Scenario
Lewis Gandolfi was pleased with his plans for teaching a lesson on estimating with a jar of pennies. He had planned it carefully so all his third-graders would (1) actively participate in the activity, (2) feel comfortable guessing and estimating, and, (3) learn to develop various ways to arrive at the answer. As he thought about his six ELLs, he opted to mix them across groups and jotted a list of much-needed vocabulary, grammar, and discourse features to review before the lesson:

Vocabulary	Sentence Level	Discourse Level
guess estimate round off numbers range cents dollars penny	ways to express amounts using cents and dollar signs	word problems graphs

The next morning, Lewis introduced the lesson by discussing the difference between a guess and an estimate and reviewing terms and phrases from the math wall. Then Lewis showed students his jar with 300 pennies and asked them to make group guesses. He took about half of the pennies out of the jar (the students decided when it was “about half”) and asked for volunteers to count aloud in piles of ten. When a brief pause occurred after the third pile was counted, Lewis promptly counted in Italian (his grandfather’s native language) and asked if someone wanted to count to ten in another language. Before he knew it, his ELLs had counted in Korean, Spanish, Russian, Vietnamese, and Urdu, followed by two native English speakers who knew French and German. Lewis was ecstatic and grateful that his improvisation had jazzed up the activity and continued with the lesson.

---

STOP AND THINK

With the information provided, how do you think Lewis’s lesson proceeded? Why? What would you do to plan a lesson on a topic like this one?

Mathematics Education and The Common Core State Standards

There are many potential challenges for ELLs in the mathematics classroom, including:

• In many countries school mathematics curricula emphasize calculations, not communicating mathematical thinking.
• Many students have never seen or worked with manipulatives and might not take a lesson using manipulatives seriously.
• In some countries, periods are used instead of commas when representing large numbers, and commas are used instead of periods when representing decimal numbers.
• Many ELLs are familiar with the metric measurement system and are unfamiliar with measurements like feet, pints, miles, ounces, etc.
• Students must read mathematics not only from left to right, but also right to left, up and down, and diagonally (in the case of tables, diagrams, and graphs).
• Some students are used to learning mathematics by rote memorization.
• In some countries, word problems are introduced in the upper grades.
• Estimating, rounding, and geometry are first taught in the upper grades in many countries.
• There are many distinct vocabulary terms used only in mathematics.
• Mathematics textbooks are tightly packed with concepts.

The Common Core State Standards (CCSS, 2010) help to address these issues by defining grade-level expectations that lead to the preparation of students for college and careers. The CCSS for Mathematics contain both content and practice standards that define what students should understand and be able to do. These standards do not dictate curricula or teaching methodologies, and they are not intended to be new labels for old ways of teaching mathematics. The CCSS, adopted by 45 states, emphasize three aspects: 1) coherence (thinking across grades and linking to major topics), 2) rigor (pursuing conceptual understanding, procedural skill and fluency, and application), and 3) focus (narrowing the scope of content and deepening understanding).  The Standards for Mathematical Practice describe ways in which students increasingly interact with content as they grow in math­ematical maturity and expertise throughout their schooling (CCSS, 2010). These practices rest on important processes and proficiencies in mathematics education and work in tandem with the mathematics standards in supporting instruction.  The eight Mathematical Practices, listed below, should function as essential habits of mind and action that should guide curriculum, pedagogy, and assessment for all K-12 students.

1. Make sense of problems and persevere in solving them.
2. Reason abstractly and quantitatively.
3. Construct viable arguments and critique the reasoning of others.
4. Model with mathematics.
5. Use appropriate tools strategically.
6. Attend to precision.
7. Look for and make use of structure.
8. Look for and express regularity in repeated reasoning.

Awareness of the language of mathematics will play a pivotal role in the implementation of each mathematical practice.  Let’s look at practice 6, “attend to precision.” The main focus is on using precise language in speech, in written symbols, and in specifying the nature and units of quantities in numerical answers, graphs, and diagrams. The term precision, however, can be interpreted differently, particularly in reference to ELLs. Judit Moschkovich (2013) requests that teachers of ELLs consider when and how to focus on precision. She also reminds us that “precise claims can be expressed in imperfect language and that attending to precision at the individual word meaning level will get in the way of students’ expressing their emerging mathematical ideas” (p. ix).  A word of caution:  precision in relation to the language of mathematics should not be reduced to understanding individual word meanings; teaching the top eight words for the lesson will not help students understand mathematical concepts and develop the necessary critical thinking skills (Ernst-Slavit & Slavit, 2013; Slavit & Ernst-Slavit, 2007). Rather, “attending to precision” will require educators to strategically select their level of precision.  Consider the following suggestions outlined by Ernst-Slavit and Slavit (2013) for helping students be successful in the mathematics classroom as they develop precise and clear communication include:

1. becoming aware of how fancy words can both aide precision but also obscure meanings;
2. allowing students to use their native languages to enhance communication;
3. encouraging students to express complex thought processes using linguistic simplicity; and
4. helping students develop metalinguistic awareness, that is, the ability to consciously reflect on the nature of language—the language of mathematics.

For suggestions on how to promote academic language development in the implementation of the eight Standards for Mathematical Practice in the CCSS, see Gottlieb & Ernst-Slavit (2013). As will become apparent, learning the academic language needed to succeed in the mathematics classroom is indeed a complex process that involves multiple features, modes of communication, and representations.

STOP AND DO

To unpack what students should know and be able to do, read the mathematical practices at http://www.corestandards.org/Math/Practice/. Highlight what students need to know and how they might demonstrate that knowledge. Reflect on the role that language plays in how students will access and demonstrate that knowledge. 

The Specialized Language of Mathematics

This focus on real-world connections may be very different from what many of our ELLs have experienced in their mathematics classes in their countries of origin, where lessons may have involved working on algorithms, manipulating mathematical expressions, and solving “recipe-type” problems (Ernst-Slavit & Slavit, 2007; Slavit & Ernst-Slavit, 2007).

Learning to communicate mathematically necessitates a variety of skills and processes to access information, to think and problem solve, and to communicate mathematical knowledge to different audiences using multiple representations (Gottlieb & Ernst-Slavit (2014). The CCSS for Mathematics has explicit student expectations related to communicating reasoning.  Students are expected to

1. communicate their reasoning through multiple representations (e.g., pictures, words, symbols, tables, graphs, pictures),
2. engage in productive oral, written, and symbolic group work with teachers and peers,
3. explain and demonstrate knowledge using emerging language, and
4. extract meaning from written mathematic texts (Moschkovich, 2013).

Clearly, this shift in mathematical practice requires students to actively participate in mathematical discourse practices.

Placing communication at the center poses some serious challenges for students who are learning English as an additional language. Students no longer have to just come up with the correct answer to a problem now students have to explain—using phrases and sentences—how they arrived at that solution. Hence, for ELLs to achieve in mathematics, they need to acquire conceptual and procedural mathematical knowledge in addition to learning to “talk math,” that is, to use the specialized language of mathematics. If not,
A key question that must be asked is whether or not an assessment measures students’ mathematical skills or their proficiency in English. . . . ELLs must process and interpret information in a language in which they are not fully proficient to be able to perform the mathematical tasks. (Gottlieb, 2007, p. iv)

Many say that mathematics is a language by itself. This is because mathematics uses a set of meaningful symbols to express ideas using conventional English syntax. For example,

2(4 − 3) + (4 + 3x) = 33

can be read as “two times four minus three plus four plus three times x equals thirty-three.” Unlike the English language, however, where you read from left to right, in mathematics, as in the example above, you have to first complete the computations within the parentheses or brackets before you can multiply by the first number on the left.

ELLs with prior school experiences in their countries of origin may find that symbols, expressions, and methods differ from those they encounter in U.S. classrooms. These barriers become increasingly challenging as students engage in story problems that can be worded in many different ways. Although there are many similarities among number systems across the world, mathematics (particularly as taught in schools) may not be a universal language for all. See Figure 9.1 for selected examples.

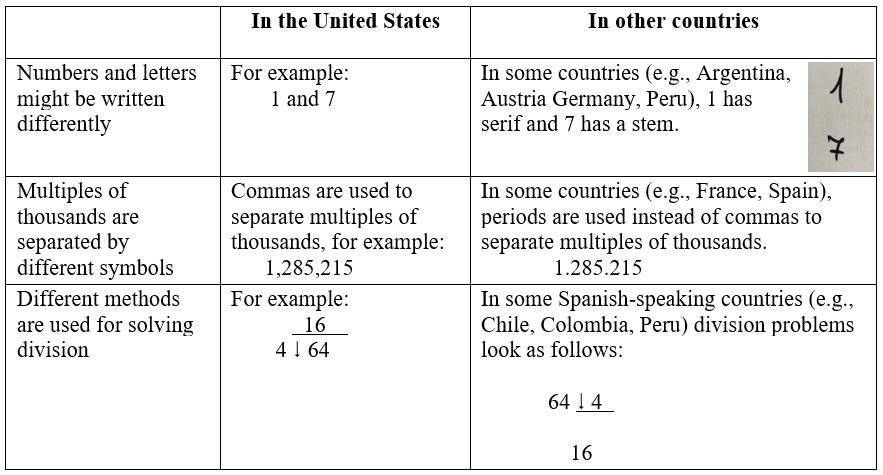
Figure 9.1 Selected examples of different representations and computing methods.

ELLs also encounter difficulties when attempting to translate a mathematical concept expressed in words into a concept expressed in symbols. For example, the algebraic phrase

the number a is five less than the number b

is often translated into

a = 5 − b

when it should be

a = b − 5

The development of the mathematics register is a critical component of developing mathematical understanding in all students, including ELLs. In this chapter, we discuss different types of vocabulary, unique syntactical features at the sentence level, and forms of discourse used in the teaching and learning of mathematics.

Word/Phrase Level

The mathematics register^[1] includes a variety of words, phrases, and expressions. As discussed in Chapter 1, these words and expressions can be classified according to three categories: general academic vocabulary, specialized academic vocabulary, and technical academic vocabulary. Figure 9.2 presents definitions and examples for each category.

Vocabulary Type	Definition	Examples
General academic vocabulary	Terms used in the mathematics classroom and in other subjects	combine describe consequently
Specialized academic vocabulary	Terms associated with mathematics	quotient least common denominator angle
Technical academic vocabulary	Terms associated with a specific mathematics topic	perfect numbers quadratic equations hypotenuse

Figure 9.2 Types of vocabulary in mathematics.

In addition, Wong-Fillmore and Snow (2000) list a series of words that pose many challenges for ELLs, such as terms that express various kinds of quantitative relationships, as well as everyday words that provide logical links in sentences typical to mathematical word problems. See Figure 9.3 for such words.

Words That Express Quantitative Relationships		Words That Link Phrases and Sentences and Express a Logical Relationship
hardly scarcely roughly rarely next last most	less longer older younger least higher many	since unless almost probably exactly not quite always never	if because unless alike same different from opposite of whether

Figure 9.3 Problematic words for English learners commonly used in mathematics textbooks and classrooms.

Another challenging aspect for ELLs is the use of many different words to refer to the same mathematical operation. See Figure 9.4 for examples. Teaching students to identify key words in word problems and displaying them prominently will assist students in identifying the kind of operation they need to pursue.

Mathematical Operation	Examples of Different Terms with Similar Meanings
Addition	add, plus, combine, sum, total of, more than, increased by, greater than, altogether, in all
Subtraction	subtract, minus, less, less than, fewer than, decreased by, difference, lower, take away from, shorter, diminished by, are left, remain
Multiplication	multiply, time, product, as a factor, twice, double, triple, groups of
Division	divide, divided by, quotient, separated in equal groups, shared equally, over, into, how many groups
Equal	Action context: is, are, result, make, become Relational context: same as, equivalent

Figure 9.4 Different Terms that Signal the Same Operation.

Representing information in nonlinguistic ways is also an important consideration when “talking math” (Lemke, 1990). For example, the idea of slope can be expressed using graphs of lines, algebraic symbols and formulas, tables of values, or contextual information (e.g., “the fixed cost of an item is the slope of a cost function for that specific item”). In addition, a variety of linguistic expressions are commonly used to refer to the general concept of slope, including rate of increase/decrease/change, linear change, degree of inclination, and rise over run. Students must draw from all four of the vocabulary types (general academic vocabulary, specialized academic vocabulary, technical academic vocabulary, and nonlinguistic expression) when participating in mathematical conversations of this kind.

As all teachers of mathematics know, specific language considerations are also needed because of the precise meaning of mathematical terms; for example, slope is a “rate of change,” but not all rates of change have a slope. Hence, all students, particularly ELLs, need to be made especially aware when their language can be imprecise and when it must be precise.

STOP AND DO

Many common English words and terms have unique meanings in mathematics. Examples include plane, face, bring down, net, and negative. Add other terms to this list. How would you help students learn the differences among their meanings?

Sentence Level Features

At the sentence level, there are language patterns and grammatical structures specific to mathematics. These include the use of logical connectors (e.g., consequently, however) that in regular usage signal a logical relationship between parts of a text, but in mathematics signal similarity or contradiction. The use of comparative structures (e.g., greater than and less than, n times as much as) and prepositions (e.g., the temperature fell . . . to 15 degrees, by 15 degrees, or from 15 degrees; divided by, divided into) pose serious difficulties for students who are trying to learn language and content simultaneously. In a 2007 article, Irujo outlined how particular sentence structures may affect meaning construction. Figure 9.5 summarizes those findings.

Sentence Structure	Examples
Passive Verbs In passive sentences, the thing receiving the action is the subject of the sentence and the thing doing the action is optionally included near the end of the sentence.	Which number is represented by the shaded part of the figure? (A drawing shows a circle with six parts; four are shaded) An ELL thinks: “No number is by the shaded part of the figure.” Which is read one million, five thousand, seventy-nine? (The question is followed by four choices, one of which is 1,005,079.) An ELL may wonder: What which are they talking about? Do they want to know which person is reading this number? How much change should she have received? (Question asked at the end of a word problem about buying something and getting the wrong change.) An ELL may ask: Does this mean how much change she has, or how much change she gets?
If Clauses If can have very different meanings, depending on the context.	If you multiply 8 times 5, the answer is 40. If I take one counter out of the bag, the probability that it will be red is 1 in 2 (assuming there are 3 red counters, 2 blue counters, and 1 green counter in the bag). If we had cut the pizza into 8 pieces instead of 4, the pieces would have been smaller.
Prepositions	6 divided by 12 is 1/2 (or 0.5). 6 divided into 12 is 2. 6 multiplied by 12 is 72 (signals multiplication) 6 exceeds 12 by 6 (signals subtraction)
Lack of correspondence between symbols and the words they represent Students take each word literally rather than thinking through what it means in relation to others.	In a dictation, students are asked to write the division problem 648 divided by 8. If they write it 648 ÷ 8, they will have no problems. If, however, thinking that 648 is a large number, they choose to write it as a long division problem, they will very likely write a problem that is read as 8 divided by 648. In an algebra problem, students read the phrase the number x is 10 less than the number y. They know they have to write an equation in order to solve the problem. So they write x (“the number x“) = (“is”) 10 – (“10 less than”) y (“the number y“). They never realize that the resulting equation, x = 10 – y, should really be x = y – 10.
Long, complex sentences Mathematical texts often use several phrases and clauses within the same sentence.	In a problem about how many 7- to 10-minute speeches could be given in a 2-hour class, students are asked: Which of the following is the best estimate for the total number of student speeches that could be given in a 2-hour class? This question contains a complex noun phrase, which contains a complex prepositional phrase, which contains a relative clause construction, which contains a passive construction. (Bielenberg & Fillmore, 2004-2005)

Figure 9.5 Selected examples of complex sentence structures in mathematics.
Source:  Adapted from Suzanne Irujo (2007). So just what is the academic language of mathematics?  ELL Outlook.

Discourse Level Features

This section discusses three areas of language difficulties: density of mathematics textbooks, word problems, and teacher talk. First, mathematics texts have a denser concentration of abstract concepts when compared to other texts. Students cannot read a mathematics textbook like a newspaper or novel. The conceptual density is too great—even when compared to textbooks in other content areas. Mathematics texts are highly connected, and each word and phrase is important to the process (Zwiers, 2008). In other words, when it comes to language, mathematics textbooks are both wonderful and dreadful. Wonderful because they are concise and to the point.  Dreadful because every single word, no matter how big or small, is packed with information. Skimming through mathematics books is not an option!

Another characteristic of math textbooks is that they often expand a basic problem into more sophisticated versions illustrating new concepts. For example, in one section of a mathematics book, students were asked to calculate the perimeter of a park enclosing three skateboard rinks.  Then, in the next section, they were asked to calculate the perimeter for the same park, this time with a different polygon shape, then they were to repeat the calculations using a fence with curves, and so on. This kind of threading, while helping students build on what they already know, may pose challenges to students who were not able to complete the task the first time.

Second, word or story problems, pervasive in the K-12 curriculum, can pose difficulties, such as in the following example by Ernst-Slavit (2015):
A certain construction job usually takes four workers six hours. Today one worker called in sick, so there are only three workers. How long should it take them to do the job?

Solving this problem requires awareness of the challenges in this story problem for ELLs.  Let’s explore some of these challenges: First, “A certain construction job” does not allow students to visualize the kind of job, which is important for helping students think through the problem. Second, the word “take” has over 100 different meanings. Third, “four workers six hours” is extremely concise and presents numbers as words.  Fourth, “called in sick” is an idiomatic expression and ELLs might not be able to decipher its meaning.  Fifth, “How long should it take” can be confusing since “long” here is asking for a unit of time, not a unit of length.  In addition, students might understand “should it take” as an obligation, rather than what is probable.

Clearly, word problems can be confusing for ELLs at several levels—in terms of language, and in relation to cultural knowledge.  Figure 9.6 illustrates select confusing aspects of the language used in word or story problems.

Confusing Aspects	Examples
Same pronoun is used to refer to different subjects.	Suppose you and three friends buy a large pizza. You each pay with a $5 bill. The pizza costs $12.75. You will also pay $.83 tax on the pizza. How much change will you and your friends get? (Houghton Mifflin’s Math Central, 2001, p. 287)
Unclear directions: Will the friend start on the pane 1 of window 1 or on pane 3 of window 1? Will he or she then move to window 2 or continue in window 1? Is the comparison among the three friends or between the “one friend” and the “two of you”? What is a “pane”?	There are four windows in the attic and each window has eight panes of glass. One friend cleans every third pane. Two of you clean the rest. Who cleans the least number of panes? (Houghton Mifflin’s Math Central, 2001, p. 241)
Use of several small words: These commonly known words (underlined) take a specialized meaning that is particular to mathematics.	A rock is dropped from a height of 200 feet. During its fall, the rock’s height h (in feet) is given by h = −16t2 + 200 where t is the time in seconds. Find the height when t = 0, 1, 2, 3, and 3.5 seconds. When does the rock hit the ground? (McDougal Littell’s Math Concepts and Skills, 2007, p. 623)
Shifting subject referents	Your grandmother started a college fund for her grandchildren 15 years ago with an investment of $15,000 at an annual interest rate of 6½%. Find the balance of the account if the account earns simple interest. (McDougal Littell’s Math Concepts and Skills, 2007, p. 378)

Figure 9.6 Examples of issues with word problems.

Pointing out some of this problematic usage in books and texts and giving explicit instruction in reading and writing word problems are ways of teaching ELLs how to grapple with the unique grammatical features of the language of mathematics. In addition, the use of warm-up activities using mathematical language can give students practice in sentence construction.

Last, a word on teacher talk. Ernst-Slavit and Mason (2011) point to the difficulties teachers may have in clarifying problematic terms and expressions in an ongoing and systematic manner. In their research, they found that even teachers who were aware of the linguistic challenges faced by ELLs and who explicitly discussed troublesome usages, such as synonyms (change, convert) and homophones (two, to, too), missed other potential sources of confusion for their students.

When teachers oversimplify their language to accommodate students’ lack of proficiency in English, students may not encounter enough opportunities to develop and practice mathematical language (Irujo, 2007). The line between too much simplification and not enough is a fine one, and the need for it varies from student to student. However, with preplanning, intentional teaching, and cumulative experience, educators can become skilled at distinguishing and applying the nuances of making the language of mathematics more accessible to all students.

Teaching Strategies for Learning and Talking Mathematics

The discussion above was intended to provide information to assist educators in better understanding the language abilities and needs of their ELLs. But we still must ask, “How do mathematics teachers teach their students mathematical thinking if their students communicate minimally in English?” or “How do I reach my ELLs?” Although there are no simple answers for these questions, the truth is that, in many mathematics classrooms, teachers are using a variety of instructional strategies that have proven useful to reaching all students, and in particular those who are learning English as a second language or third language.

Below we provide selected strategies that support ELLs as they learn how to talk math using the mathematics register, how to do math, and how to think mathematically.

Use a Variety of Instructional Formats and Supports

Students learn in many different ways. Classroom activities can be structured to support many learning styles and strengths. For all students, particularly for ELLs, the use of instructional supports (e.g., discussing a graphic organizer, working with a partner, using manipulatives) increases the understanding of the topic at hand. Below is a list of suggestions:

• Design multisensory lessons (visual, auditory, tactile, kinesthetic).
• Use visuals (graphs, charts, diagrams, models) when possible.
• Point to or explicitly connect terms with a visual representation.
• Design hands-on activities.
• Use different technologies.
• Vary groupings throughout the lesson (independent work, pairs, groups, whole class).
• Use real-life problem-solving situations to teach new concepts.
• Make connections across content areas whenever possible.

STOP AND DO

Create a graph online with the help of the National Center for Education Statistics at http://nces.ed.gov/nceskids/createagraph/ to visually represent a mathematical concept.
For examples of graphic organizers in math, visit the Michigan Council of Teachers of Mathematics at https://www.mictm.org/index.php/resources/links/260-graphic-organizers

Introduce New Vocabulary in a Thoughtful and Integrated Manner

Vocabulary is best taught not as a separate activity but as part of the lesson. For example, students who memorize the definition of cube without solving a problem or participating in a discussion involving cubes often have a superficial understanding of this term. Manipulatives and visual aids, such as pictures, graphic organizers, charts, and bulletin boards, are good support for these conversations. Recent research indicates that vocabulary instruction must occur in authentic contexts, where students have a variety of opportunities to learn how target words interact with, garner meaning from, and support meanings of other words (Nagy & Townsend, 2012).

Identify and Highlight Key Words with Multiple Meanings

In addition to the problematic words and phrases discussed earlier, ELLs can have difficulty with words that have multiple meanings in social and academic language or in other content areas. For example, the word table can refer to a times table for multiplication facts or a table of values for graphing functions. Table may also have very different meanings and usages in nonmathematical contexts, such as a timetable in social studies, table of contents in language arts, water table in physical science, and periodic table in chemistry. Identifying and carefully planning the use of any such words that you anticipate using in a lesson can support students’ efforts to follow the subsequent line of discourse.

STOP AND DO

Review the extensive list of mathematics words and their definitions at https://www.mathwords.com/a_to_z.htm. Choose one that has multiple meanings and plan how you might teach it.

Modify Speech

One important aspect of teaching ELLs includes providing comprehensible input (Krashen, 1981), that is, when teachers modify their speech to facilitate communication and enhance students’ understanding. Often, however, modification is understood as meaning “simplification,” and while that strategy might be helpful in the short term, it is not the only adjustment teachers can make to promote understanding. Below is a list of additional suggestions:

• Enunciate clearly and slowly without speaking louder (ELLs are not hard of hearing; they are second language learners).
• Pause between sentences or concepts.
• Use gestures and visuals to enhance meaning.
• Avoid using idioms and slang.
• Use key words frequently.
• Repeat, rephrase, restate.
• Particularly for difficult mathematical content, allow non-English-language group discussion or the help of teaching assistants.
• Focus on the content, not on the form, of students’ responses. Respond to inappropriately phrased language by modeling the appropriate grammatical form instead of correcting.
• Be aware that additional wait-time may be needed when teaching ELLs.

The concept of wait-time, a phrase coined by Mary Budd Rowe (1972), refers to the time students are given to respond to a question posed by the teacher. Studies by Rowe and others (see, for example, Ernst-Slavit & Pratt, 2017) showed that, in most classrooms, students were given no more than 1.5 seconds before teachers continued talking or students provided an answer. In classrooms were teachers paused between 3 and 7 seconds after asking high-level questions, students responded more thoughtfully and their achievement increased. With adequate wait-time and other speech changes, such as simplifying the language used rather than the mathematical concepts taught, teachers can preserve the integrity of the content while making language comprehensible.

Use Preview and Review

This technique provides a lesson introduction (which can be given to all students or only to ELLs) via a handout, an outline of the entire lesson on the board or overhead, and a list of key words. This preview provides context for the lesson, and small-group discussion can support any of these steps. After the lesson, a review of its main aspects, including both key content and language features, can be provided to further clarify or reinforce learning goals as well as key terms.

Kristie, a middle school teacher, uses the preview and review technique in all of her classes, including those with ELLs. Her use of preview is extended through the use of a “hula skirt,” a piece of paper folded down the middle and cut horizontally into four or five strips on each side. The students are asked to write key terms and definitions on the left and provide a visual on the right. These terms are then used during the lesson, and the students make regular use of the “hula skirt” throughout. Kristie states: “For my ELLs, I always try to use different modalities to get them to understand the vocabulary. The hula skirt is kind of fun, and it gets them to write a definition and connect it to a visual. I tell them I am bad at Pictionary, you know, like stick figures and stuff, so the drawing doesn’t have to be perfect. But it really connects them to the meaning of the word.” Kristie also uses the “hula skirt” for a game modeled on Jeopardy by having one of a pair of students fold and cover the strip with the illustration and asking the other to provide either the word or definition (Ernst-Slavit & Slavit, 2007).

Search for Cognates: Validating Students’ Languages and Cultures

Cognates are words related in origin and occur most often in English, Greek, Latin, and German, although Farsi and Turkish have English cognates, for example, temperature–temperatura (Spanish); citizen–citoyen (French); mother–Mutter (German); inflation–enflasyon (Turkish).  False cognates, on the other hand, are terms that appear to be similar in two languages and may have similar roots but their meaning is different. Examples of false cognates in English and Spanish are library–librería (bookstore); embarrassed–embarazada (pregnant); exit–exito (success); pan–pan (bread).

Research indicates that students’ home languages can play a significant role in learning complex material, including content encountered in mathematics classrooms. This is especially true when students are afforded opportunities to incorporate their home language into classroom discourse. Even teachers who do not speak ELLs’ home languages can use this strategy by giving students options for accessing books, handouts, or websites in their native languages, or working with peers or teaching assistants versed in the native languages. For example, Arthur, a middle school teacher in a building with a large number of Mexican and Central American students, builds on students’ knowledge of Spanish by using cognates. Arthur states, “My Spanish-speaking students understand more English than they realize. For example, they know círculo [circle], lateral [lateral; related to the side], cuadrado [a square or special quadrilateral], and even words like edificio [edifice], and casi [quasi; resembling something].” The use of cognates helps Arthur validate students’ first languages while, at the same time, enables students to learn language and content through vocabulary that can be easily identified in its written form.

All students come with varied experiences and knowledge, which can often lead to creative ways of solving mathematical problems. Sharing such samples of student thinking and problem solving is currently at the heart of mathematics education reform. Additional suggestions for tapping students’ knowledge include the following:

• Connect students’ prior knowledge and experiences to new learning. Find out what students already know about a topic by making a semantic web on the board. Write the topic in the center and record students’ knowledge around it.
• Integrate ELLs’ cultures into lessons whenever possible. Give students opportunities to share examples from schools in their country and different ways of learning mathematics.
• Begin a unit of study by building on students’ own questions about the topic.

Use Cooperative Learning and Promote Opportunities for Interaction

It is possible for students of diverse linguistic and educational backgrounds to work together on a task in pursuit of a common goal. Collaborative groups provide opportunities for students to hear and use the math register, while at the same time developing mathematical understandings. Depending on the students’ language proficiencies, this works very well in groups with diverse language backgrounds because students can use English to communicate with all the members of the group. Teachers can provide visuals with key words to support students with emerging language proficiency, even in groups with a variety of home languages. For example, Martha, a seventh-grade mathematics teacher with students from Latin America, Eastern Europe, and North Africa, asked her class to count on their fingers. Maddie noticed that Chimwala began counting with her thumb, others began counting with their pinkies, and most began with their index fingers. After this realization, Martha asked all her students to share in groups how they use their fingers, or any other body parts, in the counting process. Though she did not choose to do so, Martha could have extended this discussion into exploring the various algorithms for performing arithmetic on whole numbers that students bring from their various home and school cultures.

Teach Organizational and Study Skills

Students need to have organization, study skills, and learning strategies to succeed in today’s classrooms. Explicitly teaching organizational and study skills is necessary at the elementary and secondary levels. The following list of suggestions for teachers will be helpful for all students, but particularly for ELLs:

• Demonstrate how to read a mathematics textbook.
• Point out key sections and resources in the textbook.
• Teach students how to organize notebooks and binders and record homework assignments.
• Teach study and test-taking skills.
• Teach note-taking skills. For beginner English language learners, copying notes is an effective way to begin learning writing conventions.

Create an Atmosphere for Risk Taking and Making Mistakes

Finally, learning a second language, including the mathematics register, has an affective base; that is, when students are motivated, feel at ease, and view their goals as reachable, then learning is enhanced. Students need to be encouraged to ask questions and take risks; making mistakes is part of learning. If students’ answers are not correct or if students are not able to follow the emerging lines of discourse, patience may be needed to ensure that student risk taking and participation will continue.

---

Scenario Conclusion
Lewis’s lesson was a success! After the spontaneous demonstration of multilingualism in his class, Lewis asked groups to estimate the total number of pennies and recorded the information on a chart under his document camera. Students continued to work in groups to produce their own charts by ordering the numbers. Other activities for this and the following day included: (1) finding the differences between the guesses and estimates, (2) rounding the numbers to the nearest ten or hundred, (3) finding the difference between the ranges in each column, (4) expressing the guesses in different forms using cents and dollar signs, (5) generating word problems using data; and (6) discussing what you could buy with that amount.

---

Conclusion

Mathematics is not limited to computation; it is very much dependent on the language in which it is taught. Current mathematics standards require students to apply computational skills in a variety of real-life problem-solving situations, read and solve word problems, communicate their mathematical thinking, and collaborate with others to complete a task. These requirements demand that students learn to “talk math.” Just as archaeologists search for bones and stone materials to understand past civilizations, educators must search the resource materials for challenging words, grammatical structures at the sentence and discourse levels, and processes that may hinder understanding of mathematics. Explicit and deliberate instruction of terms, concepts, and processes—in addition to the utilization of a variety of instructional supports and classroom arrangements—can enhance mathematics instruction for all students.

---

Extensions

For Reflection

1. In your ELLs’ shoes. Recall a time when you were learning a second language. Now imagine you had to learn mathematics in that language. What would you want your teacher to do?
2. Think back. Recall your school or college days and reflect on your best and worst experiences in the mathematics classroom. What did some teachers do to foster or hinder learning? Was there an emphasis on engaging in mathematical practices? Was there explicit language instruction?

For Action

1. Adapt a lesson. Find a lesson or unit on the Internet that is appropriate to your grade level or area of interest. Check if this lesson or unit grows out of real-world problems, is relevant to your students, and focuses on teaching explicit language components needed to understand the lesson. If it does not have any of these features, what adaptations would you need to make?
2. Interview a student or an adult whose first language is not English. Find out how the student or adult learned mathematics in his or her schools. Was the emphasis on computational activities or communicating knowledge? Also, find out if, in this person’s home country, he or she uses different symbols to represent various concepts.
3. Check for more information on CCSS and Mathematics in any of the following texts:
• Common Core State Standards Mathematics at http://www.corestandards.org/Math/
• ELLs and Common Core in Mathematics (2015), a video interview with Dr. Judit Moschkovich at https://vimeo.com/123889734
• Gottlieb, M., & Ernst-Slavit, G. (2013). Academic language in diverse classrooms: Promoting content and language learning. Mathematics Grades K-2. Thousand Oaks, CA: Corwin.
• Gottlieb, M., & Ernst-Slavit, G. (2013). Academic language in diverse classrooms: Promoting content and language learning. Mathematics Grades 3-5. Thousand Oaks, CA: Corwin.
• Gottlieb, M., & Ernst-Slavit, G. (2013). Academic language in diverse classrooms: Promoting content and language learning. Mathematics Grades 6-8. Thousand Oaks, CA: Corwin.
4. Find answers. Check the following resources for more information about teaching math to ELLs.
• Celedón-Pattichis, S., & Ramirez, N. G. (2012). Beyond good teaching: Advancing mathematics education for ELLs. Reston, VA: National Council of Teachers of Mathematics.
• de Oliveira, L., Obenchain, K., Kenney, R., & Oliveira, A. (2019). Teaching the content areas to English language learners in secondary schools, Springer.
• Ernst-Slavit, G & Slavit, D. (2013, March 18). Mathematically speaking, Language Magazine. https://www.languagemagazine.com/2013/03/18/6006/
• National Academies of Sciences, Engineering, and Medicine (2018). English learners in STEM subjects: Transforming classrooms, schools, and lives. Washington, DC: The National Academies Press.

References

Bielenberg, B., & Fillmore, L.W. (2004-2005). The English they need for the test.  Educational Leadership, (62)4, 45-49.

Celedón-Pattichis, S., & Ramirez, N. G. (2012). Beyond good teaching: Advancing mathematics education for ELLs. Reston, VA: National Council of Teachers of Mathematics.

Common Core State Standards (CCSS). (2010). Common Core State Standards for Mathematics. National Governors Association Center for Best Practices, Council of Chief State School Officers, Washington D.C.

de Oliveira, L., Obenchain, K., Kenney, R., & Oliveira, A. (2019). Teaching the content areas to English language learners in secondary schools, Springer.

Ernst-Slavit, G. (2015). Webinar on academic language: Important for ALL, essential for English language learners. Migrant and Bilingual Education, Olympia, WA: Office of the Superintendent of Public Instruction. June 10. http://www.k12.wa.us/MigrantBilingual/Webinar/AcademicLanguage6-11-15.wmv

Ernst-Slavit, G., & Mason, M.  (2011). “Words that hold us up:” Teacher talk and academic language in five upper elementary classrooms. Linguistics and Education, 22, 430-440. doi:10.1016/j.linged.2011.04.004.

Ernst-Slavit, G., & Pratt, K. L. (2017). Teacher questions: Learning the discourse of science in a linguistically diverse elementary classroom. Linguistics and Education, 40, 1-10. https://doi.org/10.1016/j.linged.2017.05.005

Ernst-Slavit, G. & Slavit, D. (2007). Educational reform, mathematics, and diverse learners: Meeting the needs of all students. Multicultural Education, 14, 20-27.

Ernst-Slavit, G., & Slavit, D. (2013).  Mathematically speaking, Language Magazine, March 18, Retrieved from: https://www.languagemagazine.com/2013/03/18/6006/

Gottlieb, M. (2007). Assessing the language of mathematics. In S. Irujo & A. Ragan, Academic language notebook: The language of math assessment handbook. Havermill, MA:  Course Crafters Publishing.

Gottlieb, M., & Ernst-Slavit, G. (2014). Academic language in diverse classrooms: Definitions and contexts.  Thousand Oaks, CA: Corwin.

Gottlieb, M., & Ernst-Slavit, G. (2013). Academic language in diverse classrooms:  Promoting content and language learning. Mathematics Grades K-2. Thousand Oaks, CA: Corwin.

Gottlieb, M., & Ernst-Slavit, G. (2013). Academic language in diverse classrooms:  Promoting content and language learning. Mathematics Grades 3-5. Thousand Oaks, CA: Corwin.

Gottlieb, M., & Ernst-Slavit, G. (2013). Academic language in diverse classrooms:  Promoting content and language learning. Mathematics Grades 6-8. Thousand Oaks, CA: Corwin.

Irujo, S. (May/June 2007).  So what is the Academic Language of mathematics?  ELL Outlook. http://mrwaddell.net/blog/uploadpics/Made4MathVocab–Reading-in-Math-research_116CA/What.is.the.language.of.mathematics.-.MayJune2007.pdf

Krashen, S. D. (1981). Second language acquisition and second language learning. Pergamon Press, Inc., Oxford.

Lemke, J. (1990). Talking science: Language, learning, and values. Norwood, NJ: Ablex.

McLaughlin, B., & McLeod, B. (1966, June). Educating all our students: Improving education for children from culturally and linguistically diverse backgrounds (Vol. 1). Santa Cruz, CA, and Washington, DC: National Center for Research on Cultural Diversity and Second Language Learning.

Moschkovich, J.N. (2013). Preface. In M. Gottlieb & G. Ernst-Slavit (Series Eds.), Academic language in diverse classrooms: Mathematics series (pp. vii-xi). Thousand Oaks, CA: Corwin.

Nagy, W., & Townsend, D. (2012). Words as tools: Learning academic vocabulary as language acquisition. Reading Research Quarterly, 47(1), 91-108 https://doi.org/10.1002/RRQ.011

National Academies of Sciences, Engineering, and Medicine. (2018). English learners in STEM subjects: Transforming classrooms, schools, and lives. Washington, DC: The National Academies Press. Doi: https://doi.org/10.17226/25182

Rowe, M. (1972). Wait-time and rewards as instructional variables, their influence in language, logic, and fate control. Paper presented at the National Association for Research in Science Teaching, Chicago, IL, ED 061 103.

Slavit, D., & Ernst-Slavit, G.  (2007). Two for one: Teaching math and English to English language learners. Middle School Journal, 39(2), 4-11.

Wong-Fillmore, L. & Snow, C. (2000). What teachers need to know about language. Washington, DC: Center for Applied Research. Retrieved from: https://files.eric.ed.gov/fulltext/ED444379.pdf

Zwiers, J. (2008). Building academic language: Essential practices for content classrooms. San Francisco, CA: Jossey-Bass.

---

1. In linguistics, a register refers to a variety of a language used in a particular context and for a particular purpose. ↵