Mathematicians, biologists, engineers and may others use sequences when modeling real world data. Each discipline has preferred ways to work with describing how to calculate each term of a sequence.

You may have seen this famous sequence 1, 1, 2, 3, 5, 8, 13,; it is called the Fibonacci sequence. It is an infinite sequence that has shown up in nature in many different areas.

Figure 1. Ammonite Fossil. The size of each chamber follows the Fibonacci Sequence.
Photo by Kimberly McGinley Vincent

J5 Research the Fibonacci sequence for appearances in nature. First find an image of the bottom of a pinecone or a sunflower.  Print the image and draw the spirals that represent terms of the Fibonacci sequence and describe how the sequence appears in your image. Second, describe two more places the Fibonacci sequence appears in nature. Proved your sources.

Mathematicians are fascinated with the Fibonacci sequence. They describe it recursively. The first two terms are 1, 1. Each term after that is found by adding the previous two terms, that is ai=ai-1+ai-2. This is useful only useful for small values of n. This recursive rule is not very useful if you don’t need to find the 100th term. So what do we do then? We find an explicit rule to describe any term in the sequence. This is what we will be exploring in this chapter.

Definitions:

A sequence is a list of objects with a particular order. A sequence can finite or infinite. A convention is to use subscripts to indicate where in the list a particular object is. For example, a1, a2 a3, a4,…is a typical way to describe a sequence. So each term is easily identified; a1 is the first term, a2 is the second term, ai is the ith term of the sequence.

An arithmetic progression is a sequence of numbers such the difference between consecutive terms is constant. The difference is typically called d. For example 0, -2, -4, -6. … is an arithmetic sequence with a difference , d= -2.

A geometric progression is a sequence of numbers such the ratio of consecutive terms s constant. The ratio is typically called r. For example, ½, ¼, 1/8, …1/2n,… is a geometric sequence with the ratio, r= ½.

J6 Give examples of each of the following:

• an increasing arithmetic sequence

• a decreasing arithmetic sequence

• an increasing geometric sequence

• a decreasing geometric sequence

We will put many examples on the board for analysis. Once you have analyzed the sequences Write a conjecture you think is always true for each of the following: (be sure to write a complete sentence that describes the type of sequence, as well as the value of the difference or ratio)

• an increasing sequence has what kind of value for d?

• a decreasing arithmetic sequence has what kind of value for d?

• an increasing geometric sequence has what kind of value for r?

• a decreasing geometric sequence has what kind of value for r?

Mathematicians, biologists, engineers and may others use sequences when modeling real world data. Each discipline has preferred ways to work with describing how to calculate each term of a sequence.

We will explore sequence in the next few tasks. These tasks will be done in small groups of 3-4 people. Cohen designed group roles to provide equal access to all students during group work. The roles provide a way for each group member to know they have a contribution to make. It is critical that as you learn to work with a new group you respect the roles and stick to them until the group has a good working relationship that values all voices.

Brief overview of leadership roles:

The above was adapted from Elizabeth Cohen’s work on complex instruction.

J7 What is the job of the person filling each of the roles? Be sure to flush out what the difference is between the facilitator and the team captain.

Task 1
Hang ‘em High

Directions: In your group work together to answer the questions in Task 1 Hang ‘em High. Be sure the recorder shows any pictures, calculations or organization tools that represent your group’s thinking.

Hang ‘em High. Eco Green Hotel is conserving energy so they hang all the pillowcases on the clothes line to air dry. To fit more pillowcases on the line the housekeepers do two things: 1. they hang the pillowcases by the short end and they hang the pillowcases so one clothespin is holding the corner of two different pillowcases. See the picture below.

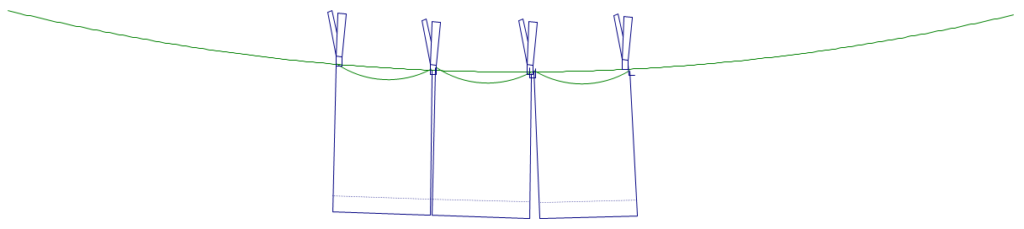
How many clothespins would be needed for 1 pillowcase? 2 pillowcases? 3 pillowcases? What if the hotel had a really long clothes line how many clothespins would be needed for 125 pillowcases?

How many clothespins would be needed for n pillowcases where n is any natural number?

Write a sequence that the ith term represents the number of clothespins needed to hang the first i pillowcases. Is this an arithmetic, geometric sequence or nether? Explain. If it is an arithmetic sequence give the first term, and the difference. If it is a geometric sequence give the first term and the ratio.

Debrief of Task 1: We will have a large group debrief before moving on to the next task. We will discuss multiple representations, recursive and explicit rules and other math concepts that can provide review or introduction to many concepts involving functions. We will make a list of such concepts during our discussion.

Student Work Hang ‘em High: Examine the responses given by middle school students below. What is good about their thinking? What needs clarification or corrections? Why? Overall, do they demonstrate understanding of the concept? What can they do to improve their communication of this understanding?

Student 1 Hang ‘em High

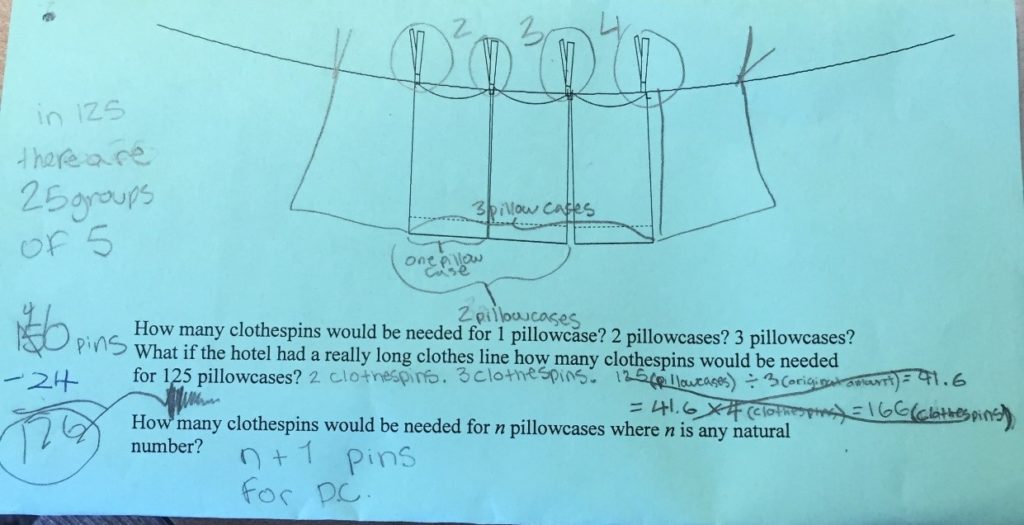
Student 2 Hang ‘em High

Task 2
Hang ‘em Low

Directions: The recorder should record any pictures, calculations or organization tools that represent your thinking in order to answer the questions below. Find both a recursive and explicit rule.

In order to comply with city code, the Eco Green Hotel had to re-hang their clothes line much lower, to keep the clothes line out of view. But the pillowcases were dragging on the ground, so now they must hang the pillowcases the long way. To keep them from drooping they must now use three clothespins per pillowcase, but they will overlap the corners to conserve clothespins, as pictured below.

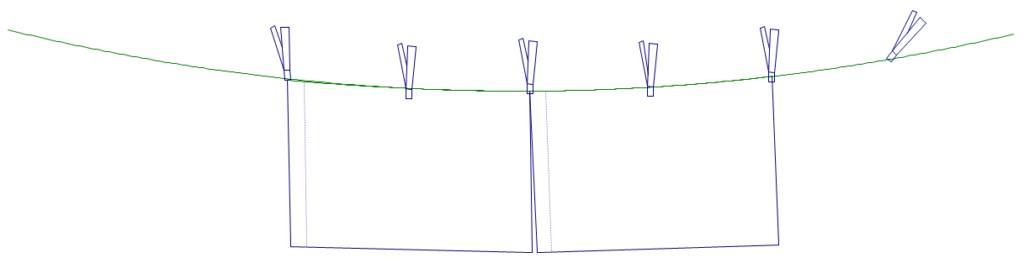
How many clothespins would be needed for 1 pillowcase? 2 pillowcases? 3 pillowcases? What if the hotel had a really long clothes line how many clothespins would be needed for 125 pillowcases?

How many clothespins would be needed for n pillowcases where n is any natural number?

Write a sequence that the ith term represents the number of clothespins needed to hang the first i pillowcases. Is this an arithmetic, geometric sequence or nether? Explain. If it is an arithmetic sequence give the first term, and the difference. If it is a geometric sequence give the first term and the ratio.

Debrief of Task 2: We will have a large group debrief before moving on to the next task. We will discuss multiple representations, recursive and explicit rules and other math concepts that can provide review or introduction to many concepts involving functions. We will make a list of such concepts during our discussion.

Student Work Hang ‘em Low: Examine the responses given by middle school students below. What is good about their thinking? What needs clarification or corrections? Why? Overall, do they demonstrate understanding of the concept? What can they do to improve their communication of this understanding?

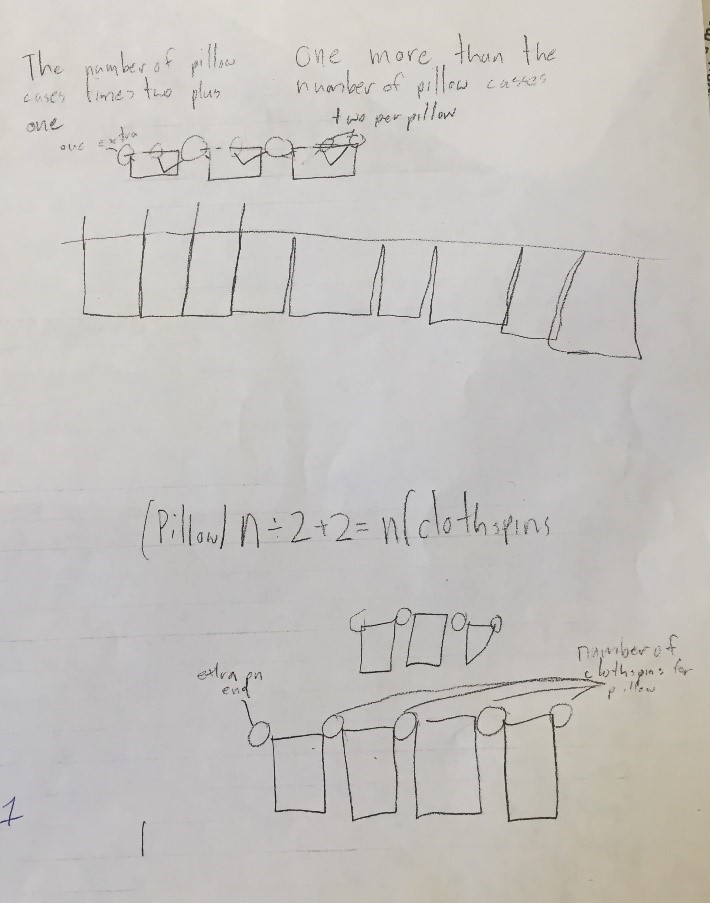
Student 1 Hang ‘em Low

Student 2 Hang ‘em Low

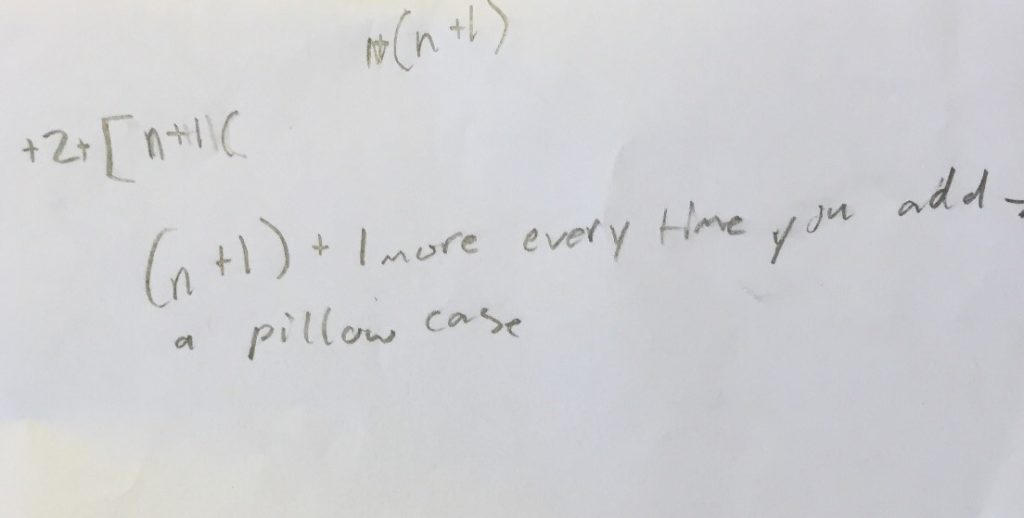
Student 3 Hang ‘em Low

Student 4 Hang ‘em Low

Student 5 Hang ‘em Low

Functions

J8. Look up the formal definition of explicit rule for a sequence. Write a formal mathematical definition. Is it a suitable definition for a middle school student who has not formally learned about functions? Explain why or why not. If it is not suitable then write or find an accurate definition that would be suitable for a middle school student.

Mathematicians define a function, f, to be a subset of A x B such that for each ordered pair in f there is exactly one ordered pair with a first element a, for all a in A. A is called the domain and B is called the codomain. This is a set theory definition that provides mathematicians with a lot of tools to prove theorems about functions. But it is not very intuitive nor useful for middle school teachers to get the ideas across to middle school students.

Informally, a function is a rule that for every element, a in the domain, A, assigns exactly one element b in the codomain, B. That is f(a)=b and each input, a in the domain, has exactly one output,. This property of exactly one describes the function as well-defined.

Let’s use arrow diagrams to illustrate examples and nonexamples.

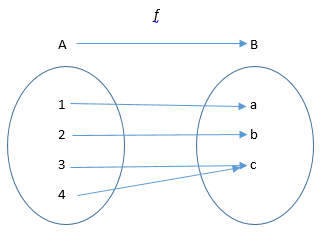
Figure 2

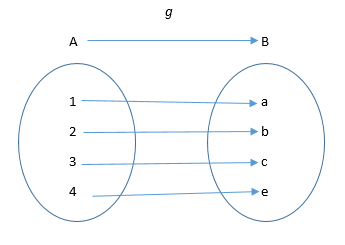
Figure 3

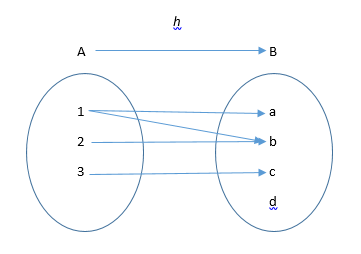
Figure 4

Examine Figures 2, 3 and 4. Which of the arrow diagrams represent a function? Why? Which do not represent a function? Why?

Name the domain and codomain in each case. In the remaining tasks we will discuss more about functions when we do our whole class debriefs.

The Range of a function is a subset of the codomain. The range of f:  is the {yin B|theres exist some a in A such that f(a)=y)} in the above examples discuss which have the range = codomain and which do not.

Models for functions: In Task 1 and Task 2 , Hang ‘em High and Hang ‘em Low you were encourage to use multiple representations. During our class debrief we discussed how the recursive rule or the explicit rule could be found in the model. This is a critical part of making models useful to students. If they are not transparent then the model will not assist in the student developing understanding. The next task will focus on seeing the rule in the model.

Task 3
Movie Madness
Posters Hung in a Row

Nan has an older brother, Bert, who works at a 14-plex movie theater. A perk to the job is he can get free movie posters. These are huge display posters used at the movie theater to promote what is currently showing. They are usually about 27 inches by 40 inches.  Bert gives many posters to Nan, who is going to hang them on the ceiling and walls of her bedroom. But they are so big that she needs to overlap the edges to make them fit.

In order to keep the posters from falling down Nan has to use four tacks on each side of a poster and three across the top. Remember she will overlap the edges just a bit.

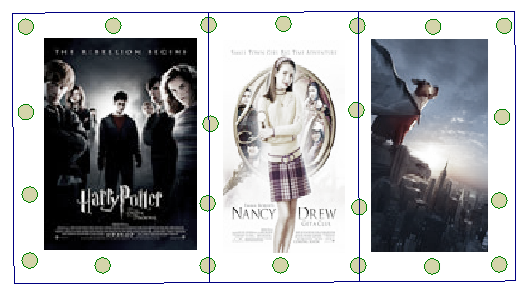
If she does one row of posters answer the following questions.

How many pushpins will she need to hang two posters? 6 posters? 11 posters? 25 posters?

Find at least two representations that allow you to find the number of pushpins needed, for n posters, without using an explicit rule.

Wait for the whole class debrief before moving on the next task.

Task 4
Movie Madness
Part II Posters Hung in Row

In order to keep the posters from falling down Nan has to use four tacks on each side of a poster and three across the top. Remember she will overlap the edges just a bit.

Below are different explicit rules middle school students came up with. Look for a pattern in the picture that the student may have used to find their rule. Are they all correct? Explain what the student might have been thinking, even if wrong.

Let n = the number of posters. P = number of pushpins needed to hang n posters

P =  4(n+1) +2n                                                  P = 10 + 6(n-1)

P = 4(n-1) + 2n                                                   P= 6n + 4

Wait for the whole class debrief before moving on to the next task.

Task 5
Movie Madness
Movie Posters in Two Rows

What if Nan hangs two rows of posters pictured like those below.

Find a rule to find the number of pushpins needed to hang n posters.

Tie your rule to the picture (the model). In your group find as many different ways to generate the rule as you can (your rules may LOOK different as in the previous task). Make a poster with all the rules. Explain how they can be seen in the context.

Wait for the whole class debrief before moving on to the next task.

Task 6
Cutting through Layers

Take your string and bend it back and forth in serpentine fashion, as pictured below.

You have one piece of string. Now, imagine that you cut across the bent string so that it passes through each “layer” like so; with each horizontal section counting as one layer.

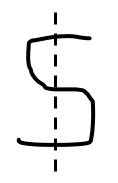
Count how many pieces of string you have now. How many pieces will you have if you make two parallel cuts? Three parallel cuts? The next cut? Forty-three cuts? Any given number of parallel cuts? Explain.

As you work make notes of your thoughts, the questions that occurred to you, what you discussed with your partner, and what you did to explore the problem. Include what you tried that worked as well as what you tried that didn’t work.

Make a poster of your data, questions, and conclusions. Post it and be ready share your results with the rest of the group.

Wait for the whole class debrief before moving on to the next task.

Task 7
Cutting through Layers

Take your string and bend it back and forth in serpentine fashion, as pictured below.

You have one piece of string. Now, imagine that you cut across the bent string so that it passes through each “layer” like so; with each horizontal section counting as one layer.

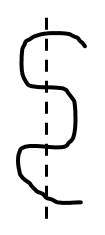
Count how many pieces of string you have now. How many pieces will you have if you make two parallel cuts? Three parallel cuts? The next cut? Forty-three cuts? Any given number of parallel cuts? Explain.

As you work make notes of your thoughts, the questions that occurred to you, what you discussed with your partner, and what you did to explore the problem. Include what you tried that worked, as well as, what you tried that didn’t work.

Make a poster of your data, questions, and conclusions. Post it and be ready share your results with the rest of the group.

Wait for the whole class debrief before moving on to the next task.

Task 8
Cutting through Layers

Take your string and bend it back and forth in serpentine fashion, as pictured below.

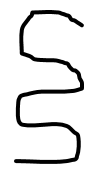
You have one piece of string. Now, imagine that you cut across the bent string so that it passes through each “layer” like so; with each horizontal section counting as one layer.

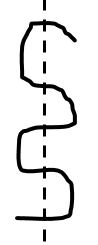
Count how many pieces of string you have now. How many pieces will you have if you make two parallel cuts? Three parallel cuts? The next cut? Forty-three cuts? Any given number of parallel cuts? Explain.

As you work make notes of your thoughts, the questions that occurred to you, what you discussed with your partner, and what you did to explore the problem. Include what you tried that worked, as well as, what you tried that didn’t work.

Make a poster of your data, questions, and conclusions. Post it and be ready share your results with the rest of the group.

Wait for the whole class debrief before moving on to the next task.

Task 9
Cutting through Layers

Take your string and bend it back and forth in serpentine fashion, as pictured below.

You have one piece of string. Now, imagine that you cut across the bent string so that it passes through each “layer” like so; with each horizontal section counting as one layer.

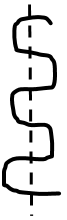
Count how many pieces of string you have now. How many pieces will you have if you make two parallel cuts? Three parallel cuts? The next cut? Forty-three cuts? Any given number of parallel cuts?  Explain.

As you work; make notes of your thoughts, the questions that occurred to you, what you discussed with your partner, and what you did to explore the problem. Include what you tried that worked, as well as, what you tried that didn’t work.

Make a poster of your data, questions, and conclusions. Post it and be ready share your results with the rest of the group.

Wait for the whole class debrief before moving on to the next task.

Task 10
Fast Food Line?

Day One: Eric is the last person in the lunch line and there are 50 kids in front of him. He is impatient, because he is soooooo very hungry. So, every time the first person in line is served, Eric sneaks up the line, by cutting in front of two people. If, at some point, he can only move ahead one person then he will just move ahead one person.

Make a prediction of how many people get served before Eric? Why do you think that? Now test your prediction.

Let’s Generalize!

What benefits are there to using this generalized rule your group came up with? Drawbacks?

If there were 20 kids served, how many kids had to be in front of Eric?

Day two: The next day Eric is even more impatient so he cuts in front of 3 kids at a time. Now how many kids are served before Eric?

What about if he cuts 4 kids at a time? Create a poster presenting all your discoveries with multiple representations used to represent your group’s thinking.

Wait for whole class debrief before moving on.

Task 11
Counting Fist Bumps

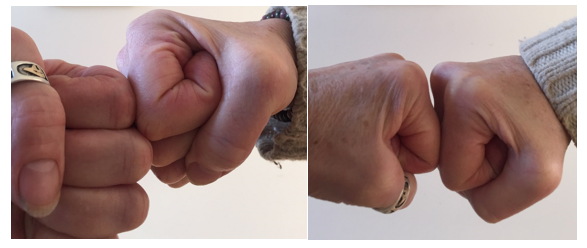
Photos by Kimberly McGinley Vincent

Hum…is there a proper way to fist bump? What does it mean? It is a sign of respect or an alternative to a high five or handshake. Our task is to count the number of fist bumps, if there are n people in a room and everyone fist bumps everyone in the room.

Whole class discussion: To answer this, we need to first agree on the rules of counting. What should these rules be?

Record the rules for counting fist bumps and then determine how many fist bumps there will be if there are n people. Use two different representations to determine your answer. Secondary folks use combinations or permutations from probability to determine the number of fist bumps for one approach and explain if and or how the pigeon hole principle might be used.

Debrief: we will compare the rules you found for the number of fist bumps and show how they are equivalent.

We will generalize and describe how to use Gauss’ trick to add a sequence of numbers two different ways. Once we have done that use Gauss’ Trick to find the following sums. We found from our fist bump counting that the sum

Gauss’ trick is to pair up terms so that each pair has the same sum so that the summation turns into a multiplication problem by counting how many pairs and multiplying the number of pairs times the sum of each pair.

The two most common rules for finding the number of fist bumps must be equal yielding the following equation: 

Mathematicians have a short cut to write the left hand side of this equation

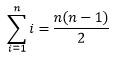
We name an index and its starting value. In this case the index will be i. The expression,  xi represents the number in the ith position. The number on the top of ∑ tells us the last value we substitute in for the index, i. To the right of sigma is an expression involving the index, i. So we take each natural number with our starting number, substitute in in for I and add to the next result when you substitute in the next value of i. In short you add up x1, x2, x3, …, xn.

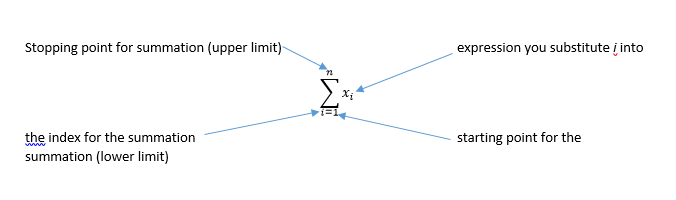
Write the sum without the sigma notation, showing the first few terms and the last few terms. Find the sum using Gauss’ trick for each of the following:

Chapter Two
Exercises

1. Below are models of the first four triangular numbers. T1 = 1, T2=3, T3 = 6, T4 = 10

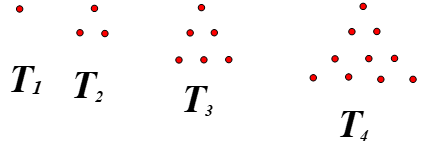
a. (10 pts.) Find a general rule for the nth triangular number, Tn. Show your thinking with the model, a written description, or a table.

b. (10 pts.) Is this an arithmetic sequence, geometric sequence or neither? Explain why or why not using the definitions of arithmetic and geometric sequences.

c. (10 pts.) Find a second rule for the nth triangular number. Explain or show your reasoning.

d. (10 pts.) Consider the series found by adding a strong of triangular numbers.      Verify this formula works for the n = 1,  n = 3 and n =10.

e. Secondary Preservice teachers Prove the conjecture from part d. using the Principle of Mathematical Induction. (see Appendix C for a review of this proof style).

2. Below are models of the first four triangular numbers. P1 = 1, P2=5, P3 = 12, that is Pn is the total number of dots in the nth figure, including dots on the inside. Notice we use P for pentagon.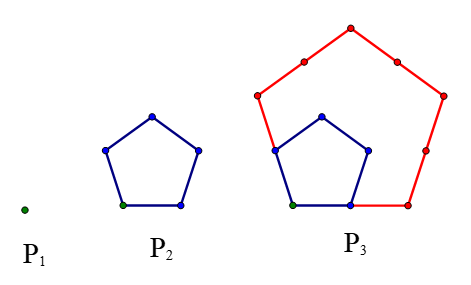 

P1 = 1,  P2=1 green dot plus 4 blue dots, P3 = one green dot + four blue dots + 7 red dots

a. (10 pts.) Draw the next pentagonal number and then create a table of values to show the recursive relationship. Describe to a middle school kid what you noticed that you had to do the previous model.

b. (10p pts) Write a recursive rule for the nth pentagonal number, Pn . So Show your thinking with the model, a written description, or a table.

c. (10 pts.) Use Gauss’ trick to find an explicit rule for Pn or the pattern to determine an explicit rule for the nth pentagonal number.

d. (10 pts.) Verify the explicit rule you found in part d works for the n = 1, n = 3 and n =10.

e. Secondary Preservice Prove that the explicit rule is is true for all natural numbers, n.

3. Given the sequence: 3, 6, 12, 24, 48, …,

a. (3 pts.) Draw a model that represents each of the first three terms of the sequence.

b. (6 pts) Write the recursive rule for the sequence?

c. (10 pts) Write an explicit rule for the nth term, support where this rules comes from with a table of values that transparently shows the pattern that generated your rule.

d. (4 pts.) Is the sequence Arithmetic? Explain why or why not.

e. (4 pts) Is the sequence Geometric? Explain why or why not.

4. Given the following sequence, 9, 27, 81, 243, 729, 2187…

a. (3 pts.) Draw a model that could represent the sequence.

b. (6 pts.) Write a recursive relation equation for a_(n+1). (Make sure you define a_1.)

c. (10 pts.) Write an explicit rule for the nth term. Show how a pattern in a table will generate the rule.

d. (6 pts.) Graph data. Be sure to define the dependent and independent variable.

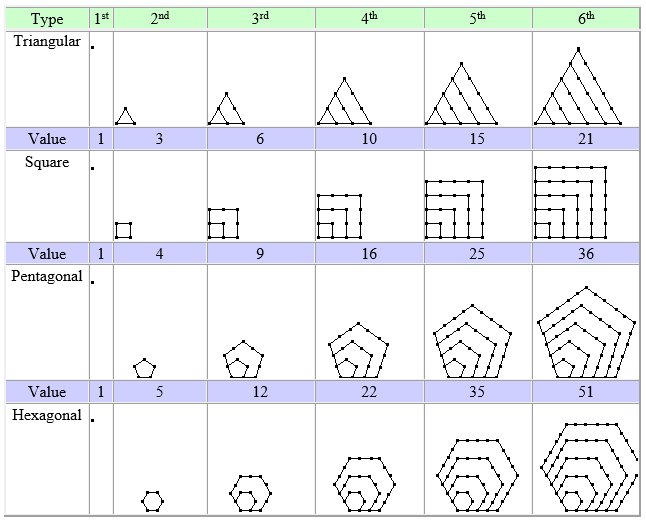5. Design a sequence of questions for middle school students about hexagonal numbers.