What is Algebraic Thinking?

What is Algebraic thinking? Is it different than algebraic reasoning? Is it different than the content of a traditional algebra course?

Journal 1: Before reading further take a few minutes to write down what you think algebraic thinking is.

A bit of Background

Economists began describing our economics as conceptual economics in the late 1990’s. Pink (2005) states that skills needed by workers no longer are limited to manipulating information or sharing expertise. Instead, “globalization that is shipping white collar work overseas, and powerful technologies that are eliminating certain kinds of work altogether—we are entering a new age. It is an age animated by a different form of thinking and a new approach to life—one that prizes aptitudes that I call “high concept” and “high touch”.”( p 121). The new age is the Conceptual Age; there is an emphasis on critical thinking, understanding, problem solving, creativity, ability to empathize and the ability to transfer knowledge. Some of these terms are relatively clear in meaning but educators always struggle to define understanding.  So, what does it mean to understand mathematics?

Before we get into what understanding is, let’s look at where we are.  In international TIMMS test results for K-12, the United States has fallen further behind in comparison to high-performing countries such as Japan and Finland (citation). For many decades the US government has been emphasizing the need to improve mathematics knowledge in order for the US to remain competitive in the global economy.  Many mathematicians and researchers consider algebra to be the gate way to higher level mathematics as well as jobs.

Access to mathematics is not necessary to keep the US competitive in the global economy but it is an equity issue based on the skills needed in the work force. Many mathematicians and math educators present various arguments for why mathematics, algebra in particular, are necessary for ALL learners to be accorded equal opportunities. For example,

Moses (2001), founder of the Algebra Project, states, “Algebra has a certain role, a certain place in the education system. Students learn how to manipulate abstract symbolic representations for underlying mathematical concepts. Now here comes history, which brings in a technology that places abstract symbolic representations front and center. These representations are tools to control the technology, and in order to use this technology to organize work you have to understand these symbolic representations and the place that society has assigned for young people to learn this symbolism–this is algebra. So, now algebra becomes an enormous barrier.” (p 15)

Goldenberg, Mark, Kang, Fries, Carter, Cordner (2015) state “Success in algebra is not merely a gateway to more advanced mathematics and science but is linked to high school graduation, college enrollment and completion , and workforce preparation. (p. x)

Journal 2: Do some research to find data to support Goldenberg’s, et al, claims. Here are some urls to get you started:

The government’s concern about the need to improve students’ mathematical understanding brought about a flurry of educational research. One result was the National Council of Teachers of Mathematics (NCTM) wrote the Principles and Standards for School Mathematics (1989). This document was the first set of standards for any discipline in the US. The second edition was published in 2000. NCTM promotes that algebra is a strand that is taught from prekindergarten all the way through high school. “The Standards for grades 6-8 include a significant emphasis on algebra, along with much more geometry than has normally been offered in the middle grades, and call for the integration of these two areas.” (NCTM, 2000 p 37)

“Algebra Standard”

Instructional programs from prekindergarten through grade 12 should enable all students to—

• • understand patterns, relations, and functions;
  • represent and analyze mathematical situations and structures using algebraic symbols;
  • use mathematical models to represent and understand quantitative relationships;
  • analyze change in various contexts.” (NCTM, 2000, p 37)

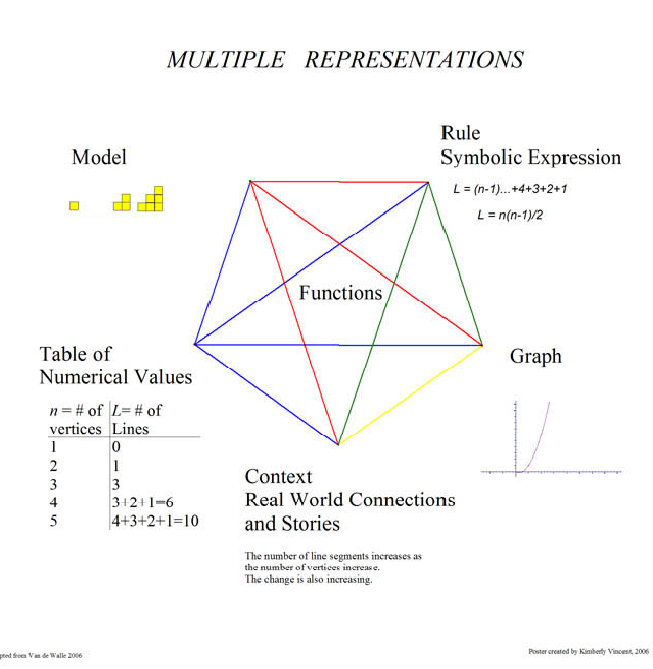
Embedded in this description is the idea of using multiple representations to study mathematics. Many researchers have discussed the need for using multiple representations. It is agreed that the use of multiple representations provide many benefits for students. Their use allows a way in to cognitively demanding tasks, for all students. It deepens understanding, and it provides the opportunity to avoid common misconceptions. Van de Walle lists five representations for elementary students: pictures; manipulative models, real-world situations, oral language, written symbols. I have adapted this to middle grades to include the formal language of algebra. The figure below shows that we can easily adapt Van de Walle’s elementary list of representation to fit our needs for generalization and abstractions.

Common Core State Standards for Mathematics identified several algebra topics in the middle grades as part of their list of critical topics. In grade 6 one of the critical topics is “writing, interpreting, and using expressions and equations”. In Grade 7 one of the critical topics is “developing understanding of operations with rational numbers and working with expressions and linear equations”. For grade 8, two of the three critical areas are relevant to algebra, “(1) formulating and reasoning about expressions and equations, including modeling an association in bivariate data with linear equation, and solving linear equations and systems of linear equations; (2) grasping the concept of a function and using functions to describe quantitative relationships”.

Both sets of standards define what students should understand and be able to do in their study of mathematics. But asking a student to understand something also means asking a teacher to assess whether the student has understood it. But what does mathematical understanding look like? One way for teachers to do that is to ask the student to justify, in a way that is appropriate to the student’s mathematical maturity, why a particular mathematical statement is true or where a mathematical rule comes from. Mathematical understanding and procedural skill are equally important, and both are assessable using mathematical tasks of sufficient richness.

CCSSM defines 8 mathematical practices (MP) (see http://www.corestandards.org/Math/Practice/ for the full description of each mathematical practice):

MP1 Make sense of problems and preserver in solving them.

MP2 Reason abstractly and quantitatively.

MP3 Construct viable arguments and critique the reasoning of others.

MP4 Model with mathematics.

MP5 Use appropriate tools strategically.

MP6 Attend to precision.

MP7 Look for and make use of structure.

MP8 Look for and express regularity in repeated reasoning.

CCSSM does not, explicitly, say what understanding is but they do state what it is not. “The Standards for Mathematical Content are a balanced combination of procedure and understanding. Expectations that begin with the word “understand” are often especially good opportunities to connect the practices to the content. Students who lack understanding of a topic may rely on procedures too heavily. Without a flexible base from which to work, they may be less likely to consider analogous problems, represent problems coherently, justify conclusions, apply the mathematics to practical situations, use technology mindfully to work with the mathematics, explain the mathematics accurately to other students, step back for an overview, or deviate from a known procedure to find a shortcut. In short, a lack of understanding effectively prevents a student from engaging in the mathematical practices.” (http://www.corestandards.org/Math/Practice/)

Teacher and Student Mindsets

NCTM (2000) states, “In this changing world, those who understand and can do mathematics will have significantly enhanced opportunities and options for shaping their futures. Mathematical competence opens doors to productive futures. A lack of mathematical competence keeps those doors closed. NCTM challenges the assumption that mathematics is only for the select few. On the contrary, everyone needs to understand mathematics. All students should have the opportunity and the support necessary to learn significant mathematics with depth and understanding.” (p5)

Mason, Graham, Johnson-Wilder (202) state “Algebraic thinking (particularly the recognition and articulation of generality) is within reach of all learners, and vital if they are to participate fully in society.” (p. ix)

Journal 3: Go to the following url http://blog.mindsetworks.com/what-s-my-mindset. Take the mindset test. What are your results? What do these results tell you about your mindset? How does this impact your view on students’ ability to learn mathematics?

The latest brain research shows that with exposure through multiple senses we can all grow dendrites. Dendrites and the firing synapses is where thought takes place. The research shows that we can all learn through this growing of dendrites and that our brain responds like a muscle; it grows stronger with use and atrophies with disuse (Dweck 2006, Boaler 2016). Dweck coined the phrases growth and fixed mindset.

Boaler (2016) states, ” Although I am not saying that everyone is born with the same brain, I am saying that there is no such thing as ‘a math brain’ or a ‘math gift’, as many believe…It is imperative for our society that we move to a more equitable and informed view of mathematics learning in our conversations and work with students. Our conversations and work need to reflect the new science of the brain and communicate to all that everyone can learn math well, not only those believed to hold a ‘gift’. This could well be the key to unlocking a different future – one in which math trauma is a thing of the past and students from all backgrounds are given access to high quality mathematics learning opportunities.” (p. 5)

Journal 4: Describe something you like about algebra. Describe something you do not like about algebra. Describe an experience that has had a major influence on how you approach algebra. Be sure to describe your approach as well as how the experience influenced that approach.

Back to what is algebraic thinking: Mathematics educators have been pondering this question for decades.

So how do we move from thinking about algebra as a content strand to algebraic thinking? There are many different lists of characteristics of algebraic thinking, depending on the researcher/educator. I will discuss a few of the approaches below and then discuss how we will attend to them in this text. Although the researchers do not find agreement nor ease in defining algebraic thinking they all have devised a list of characteristics they deem necessary.

Driscoll (1999) defines what he calls habits of mind that will foster the learning of formal algebra. Since formal algebra is often late middle school and high school these habits of mind need to be developed and continually nurtured in grades K-8. Driscoll states, “ A facility with algebraic thinking includes being able to think about functions and how they work, and to think about the impact that a system’s structure has on calculations These two aspects of algebraic thinking are facilitated by certain habits of mind.” (p1) The three habits of mind Driscoll identifies are doing and undoing, building rules to represent functions, and abstracting from computation. We will discuss these in more detail throughout the course.

Mason, Graham, Johnston-Wilder (2012) take the stand that every mathematics lesson must involve generalizing. They never clearly define algebraic thinking but they claim that “The language of algebra is used to capture and to express the idea of structure itself.” (p313). They go on to say algebraic thinking is what allows student to develop higher algebra understanding, that is to move from generalizing with numbers to “…’higher algebra’ uses the structures which are revealed by generalizing numbers, as the replacement for numbers themselves. A ‘structure’ involves both objects and operations on those objects, just as arithmetic compromises numbers, and operations on those numbers.” (p 313).

Goldenberg, Mark, Kang, Fries, Carter, Cordner (2015) describe:

• Five specific teaching ingredients are described in this book, all used in ways that develop algebraic habits of mind we want. All of the following can be adapted to a variety of educational contexts, teaching styles and core curricula:
  • mental mathematics activities that build computational fluency and strengthen executive function
  • mathematical puzzles to support algebraic reasoning, arithmetic facility, and perseverance in problem solving
  • exploration-based learning to support pattern identification and description with algebraic notation
  • broadly useful mathematical tools such as number lines and area models that offer students spatial ideas to support their understanding of numbers and algebra
  • classroom discussions that support meaningful mathematical communication and precision and that broaden problem-solving techniques. (p xi)

In this text we will focus on making conjectures, by analyzing patterns and generalizing the patterns: 1. We will build rules for functions through the process of generalizing; 2. We will be “abstracting from computation”; and 3. we will be generalizing from our understanding of numbers to build structures. You will be given a math task to complete in class in a collaborative setting (through exploration), using multiple representations, whenever possible. After completing each math task, we will discuss the different mathematical concepts that can be flushed out with different grade bands, K-9 but primarily the middle grades. This will illustrate the different ways a math task can be adapted for differential learning as well as for different grade bands.  The CCSSM middle school content standards for each math task as presented, and for some of the possible extensions, will be provided in an appendix.