How to use the Principle of Mathematical Induction
Define a predicte Pn which is typically some equation dependent on natural numbers starting at 1 .
To proof the equation is always true:
Step 1: prove the base case
That is prove the equation given in Pn is true for n= 1.
Step 2 the induction step
The idea is you pick a random starting place and show that if you use the recursive relationship you can get from the kth step to the k+1st step. This shows that if Pk is true then Pk+1 must also be true.
Explain why Step 1 and Step 2 prove Pn is always true for all n N
For each of the following cases use a table of values to convince yourself you see that the relationship is true for n = 1 , 2 and 3 at the minimum. Then Write out the “proof” using mathematics induction.
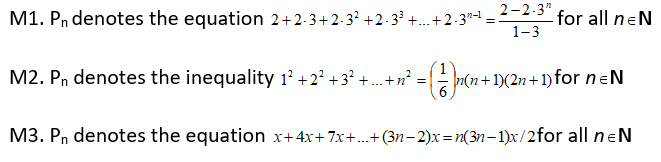
The next three are a bit more challenging.
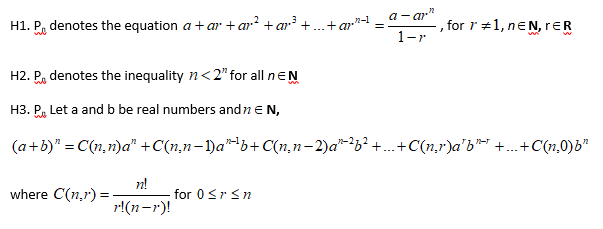
explanation
http://www.coolmath.com/algebra/19-sequences-series/09-mathematical-induction-01
more problems
http://www.cs.cornell.edu/courses/cs2800/2015fa/handouts/toronto_induction.pdf
http://mathcircle.berkeley.edu/archivedocs/1999_2000/lectures/9900lecturespdf/induction.pdf
https://people.richland.edu/james/lecture/m116/sequences/induction.html
